Traditional maze puzzles have been used a lot in data structures and algorithms research and education. The well-known Dijkstra shortest path algorithm is still the most practical method for solving such puzzles, but due to their familiarity and intuititive nature, these puzzles are quite good for demonstrating and testing Reiforcement Learning techniques.
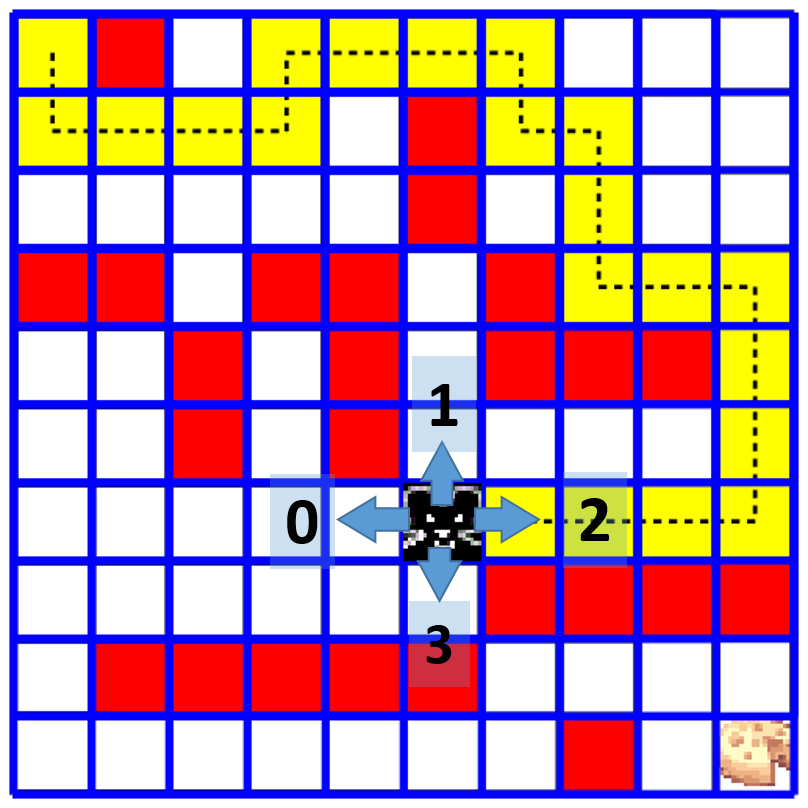
A simple maze consists of a rectangular grid of cells (usually square), a rat, and a "cheese" cell.
We will use small 7x7, 8x8, and 10x10 mazes as examples. The cheese is always at the bottom right cell of the maze. We have two types of cells: free cells (white) and occupied cells (red or black). The rat can start from any free cell and is allowed to travel on the free cells only
A framework for an MDP (Markov Decision Process) consists of an environment and an agent which acts in this environment. In our case the environment is a classical square maze with three types of cells:
- Occupied cells
- Free cells
- Target Cell (in which the cheese is located)
Our agent is a rat (or a mouse if you prefer) which is allowed to move only on free cells, and whose sole purpose in life is to get to the cheese.
In our model, the rat will be "encouraged" to find the shortest path to the target cell by a simple rewarding scheme:
- We have exactly 4 actions which we must encode as integers 0-3:
- 0 - left
- 1 - up
- 2 - right
- 3 - down
- Our rewards will be floating points ranging from -1.0 to 1.0.
- Each move from one state to the next state will be rewarded (the rat gets points) by a positive or a negative (penalty) amount.
- Each move from one cell to an adjacent cell will cost the rat -0.04 points. This should discourage the rat from wandering around and get to the cheese in the shortest route possible.
- The maximal reward of 1.0 points is given when the rat hits the cheese cell.
- An attempt to enter a blocked cell ("red" cell) will cost the rat -0.75 points! This is a severe penalty, so hopefully the rat will learn to avoid it completely. Note that an attempt to move to a blocked cell is invalid and will not be executed. But it will incur a -0.75 penalty if attempted.
- Same rule hold for an attempt to move outside the maze boundaries: -0.8 points penalty.
- The rat will be penelized by -0.25 points for any move to a cell which he has already visited. This is clealy a counter productive action that should not be taken at all.
- To avoid infinite loops and senseless wandering, the game is ended (lose) once the total reward of the rat is below the negative threshold: (-0.5 * maze.size). We assume that under this threshold, the rat has "lost its way" and already made too many errors from which he has learned enough, and should proceed to a new fresh game.
pip install pandas numpy keras matplotlib
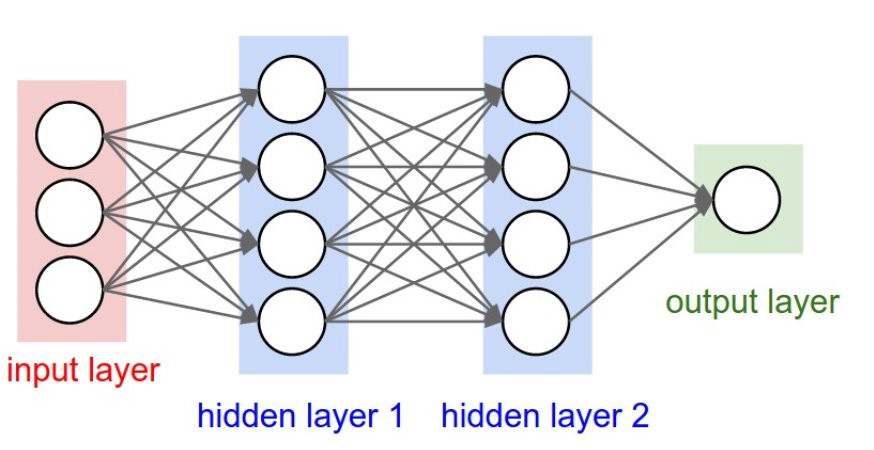
The project uses Sequential Neural Network Architecture
- Before Training
Make sure you have the following is installed:
You can get the colab link here
In the AI maze solver game, the AI used a PRelu activation function and deep Q learning with a sequential model, and was run for 1000 epochs. The accuracy of the AI in solving the maze was 81%. This result suggests that the AI was able to successfully navigate to the end goal of the maze in 81% of the cases. It is possible that the AI was able to learn and adapt to the specific characteristics of the maze, such as the layout and any obstacles or rewards present, and use this knowledge to make informed decisions about which actions to take at each step in order to reach the end goal.
There are many directions in which the use of deep Q-learning in AI maze solver games could be extended and improved in the future. Incorporating more advanced machine learning techniques: Deep Q-learning is just one tool in the AI toolkit, and there are many other techniques that could potentially be used to improve the performance of AI maze solvers. For example, techniques such as deep reinforcement learning, evolutionary algorithms, or probabilistic graphical models could be used to optimize the decision-making process of the AI agent.