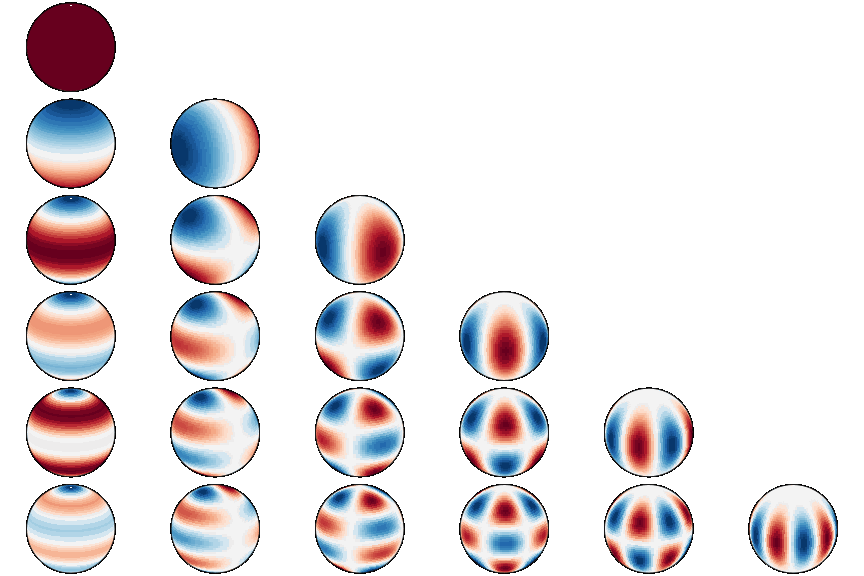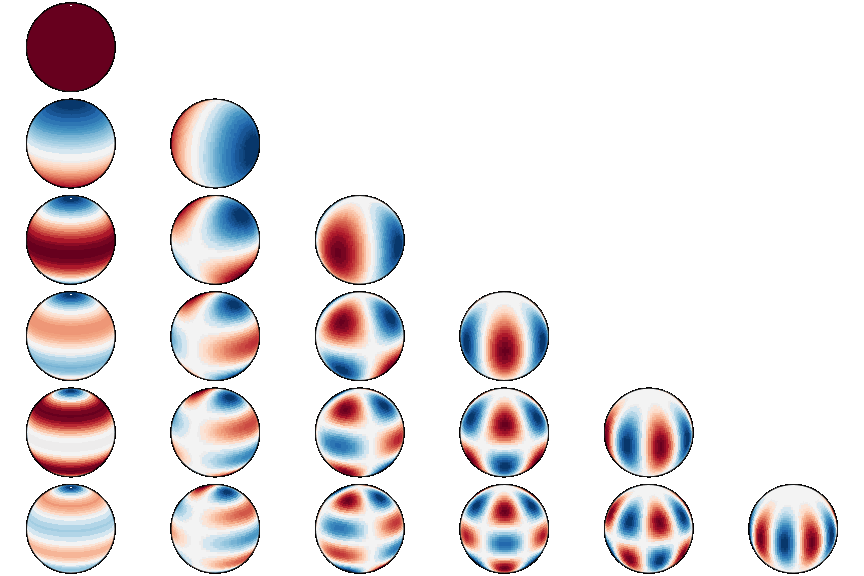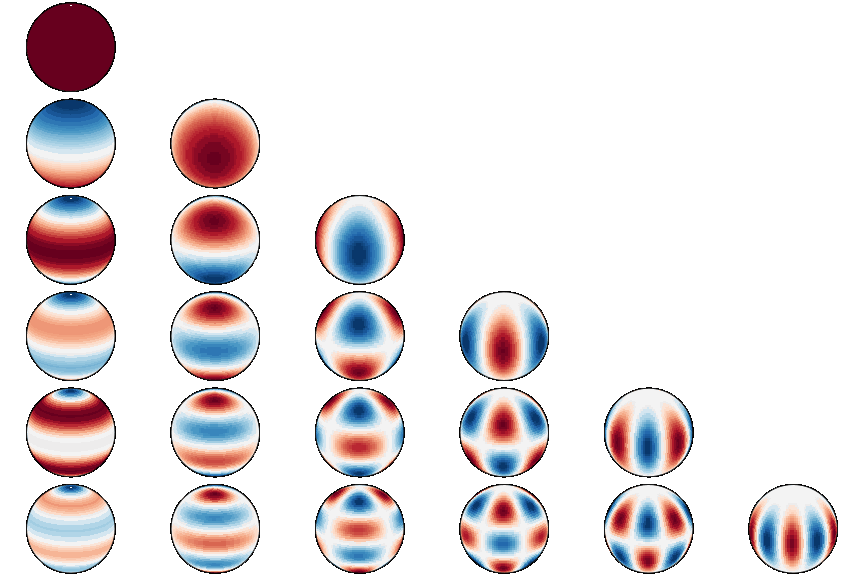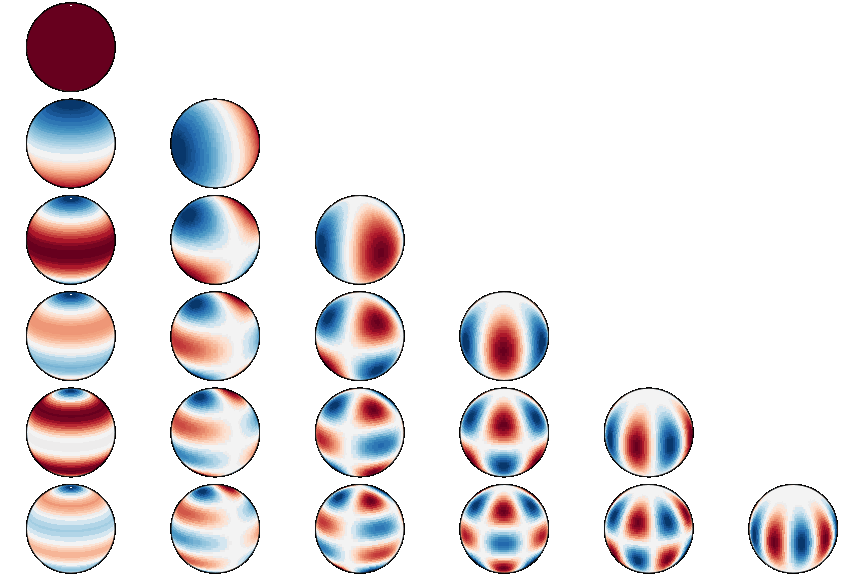Skip to content

Latest commit

 

History

History
275 lines (199 loc) · 12.9 KB

README.md

File metadata and controls

275 lines (199 loc) · 12.9 KB
Raw

torch-harmonics

Overview | Installation | More information | Getting started | Contributors | Cite us | References

tests pypi

Overview

torch-harmonics implements differentiable signal processing on the sphere. This includes differentiable implementations of the spherical harmonic transforms, vector spherical harmonic transforms and discrete-continuous convolutions on the sphere. The package was originally implemented to enable Spherical Fourier Neural Operators (SFNO) [1].

The SHT algorithm uses quadrature rules to compute the projection onto the associated Legendre polynomials and FFTs for the projection onto the harmonic basis. This algorithm tends to outperform others with better asymptotic scaling for most practical purposes [2].

torch-harmonics uses PyTorch primitives to implement these operations, making it fully differentiable. Moreover, the quadrature can be distributed onto multiple ranks making it spatially distributed.

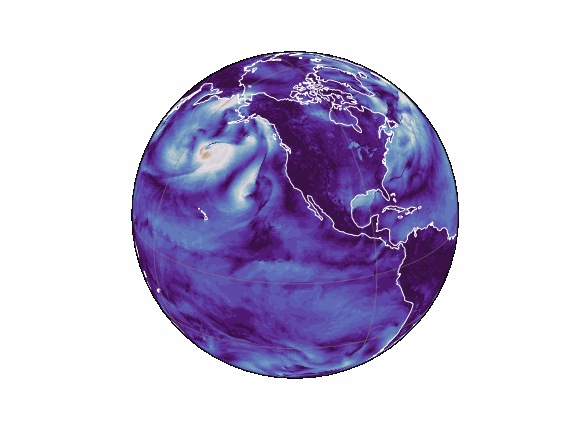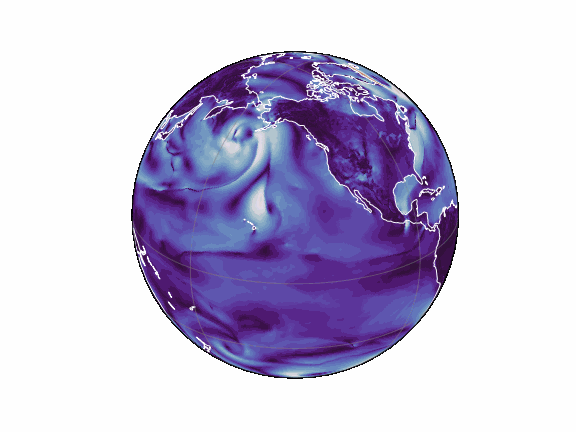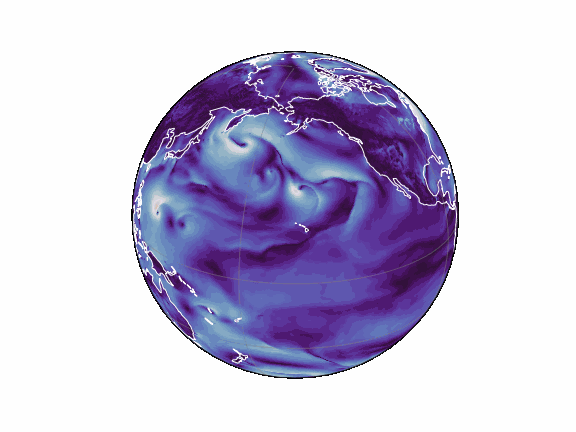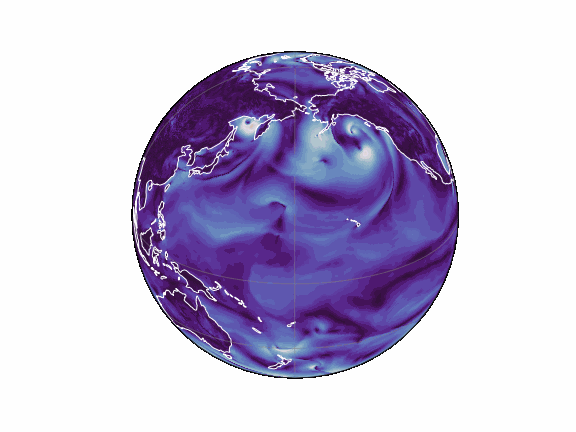
torch-harmonics has been used to implement a variety of differentiable PDE solvers which generated the animations below. Moreover, it has enabled the development of Spherical Fourier Neural Operators (SFNOs) [1].

Installation

A simple installation can be directly done from PyPI:

pip install torch-harmonics

If you are planning to use spherical convolutions, we recommend building the corresponding custom CUDA kernels. To enforce this, you can set the FORCE_CUDA_EXTENSION flag. You may also want to set appropriate architectures with the TORCH_CUDA_ARCH_LIST flag. Finally, make sure to disable build isolation via the --no-build-isolation flag to ensure that the custom kernels are built with the existing torch installation.

export FORCE_CUDA_EXTENSION=1
export TORCH_CUDA_ARCH_LIST="7.0 7.2 7.5 8.0 8.6 8.7 9.0+PTX"
pip install --no-build-isolation torch-harmonics

⚠️ Please note that the custom CUDA extensions currently only support CUDA architectures >= 7.0.

If you want to actively develop torch-harmonics, we recommend building it in your environment from github:

git clone [email protected]:NVIDIA/torch-harmonics.git
cd torch-harmonics
pip install -e .

Alternatively, use the Dockerfile to build your custom container after cloning:

git clone [email protected]:NVIDIA/torch-harmonics.git
cd torch-harmonics
docker build . -t torch_harmonics
docker run --gpus all -it --rm --ipc=host --ulimit memlock=-1 --ulimit stack=67108864 torch_harmonics

More about torch-harmonics

Spherical harmonics

The spherical harmonics are special functions defined on the two-dimensional sphere $S^2$ (embedded in three dimensions). They form an orthonormal basis of the space of square-integrable functions defined on the sphere $L^2(S^2)$ and are comparable to the harmonic functions defined on a circle/torus. The spherical harmonics are defined as

$$ Y_l^m(\theta, \lambda) = \sqrt{\frac{(2l + 1)}{4 \pi} \frac{(l - m)!}{(l + m)!}} P_l^m(\cos \theta) \exp(im\lambda), $$

where $\theta$ and $\lambda$ are colatitude and longitude respectively, and $P_l^m$ the normalized, associated Legendre polynomials.


Spherical harmonics up to degree 5

Spherical harmonic transform

The spherical harmonic transform (SHT)

$$ f_l^m = \int_{S^2} \overline{Y_{l}^{m}}(\theta, \lambda) f(\theta, \lambda) \mathrm{d} \mu(\theta, \lambda) $$

realizes the projection of a signal $f(\theta, \lambda)$ on $S^2$ onto the spherical harmonics basis. The SHT generalizes the Fourier transform on the sphere. Conversely, a truncated series expansion of a function $f$ can be written in terms of spherical harmonics as

$$ f (\theta, \lambda) = \sum_{m=-M}^{M} \exp(im\lambda) \sum_{l=|m|}^{M} \hat f_l^m P_l^m (\cos \theta), $$

where $\hat{f}_l^m$, are the expansion coefficients associated to the mode $m$, $n$.

The implementation of the SHT follows the algorithm as presented in [2]. A direct spherical harmonic transform can be accomplished by a Fourier transform

$$ \hat f^m(\theta) = \frac{1}{2 \pi} \int_{0}^{2\pi} f(\theta, \lambda) \exp(-im\lambda) \mathrm{d} \lambda $$

in longitude and a Legendre transform

$$ \hat f_l^m = \frac{1}{2} \int^{\pi}_0 \hat f^{m} (\theta) P_l^m (\cos \theta) \sin \theta \mathrm{d} \theta $$

in latitude.

Discrete Legendre transform

The second integral, which computed the projection onto the Legendre polynomials is realized with quadrature. On the Gaussian grid, we use Gaussian quadrature in the $\cos \theta$ domain. The integral

$$ \hat f_l^m = \frac{1}{2} \int_{-1}^1 \hat{f}^m(\arccos x) P_l^m (x) \mathrm{d} x $$

is obtained with the substitution $x = \cos \theta$ and then approximated by the sum

$$ \hat f_l^m = \sum_{j=1}^{N_\theta} \hat{f}^m(\arccos x_j) P_l^m(x_j) w_j. $$

Here, $x_j \in [-1,1]$ are the quadrature nodes with the respective quadrature weights $w_j$.

Discrete-continuous convolutions

torch-harmonics now provides local discrete-continuous (DISCO) convolutions as outlined in [4] on the sphere.

Getting started

The main functionality of torch_harmonics is provided in the form of torch.nn.Modules for composability. A minimum example is given by:

import torch
import torch_harmonics as th

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

nlat = 512
nlon = 2*nlat
batch_size = 32
signal = torch.randn(batch_size, nlat, nlon)

# transform data on an equiangular grid
sht = th.RealSHT(nlat, nlon, grid="equiangular").to(device)

coeffs = sht(signal)

To enable scalable model-parallelism, torch-harmonics implements a distributed variant of the SHT located in torch_harmonics.distributed.

Detailed usage of torch-harmonics, alongside helpful analysis provided in a series of notebooks:

  1. Getting started
  2. Quadrature
  3. Visualizing the spherical harmonics
  4. Spectral fitting vs. SHT
  5. Conditioning of the Gramian
  6. Solving the Helmholtz equation
  7. Solving the shallow water equations
  8. Training Spherical Fourier Neural Operators (SFNO)
  9. Resampling signals on the sphere

Remarks on automatic mixed precision (AMP) support

Note that torch-harmonics uses Fourier transforms from torch.fft which in turn uses kernels from the optimized cuFFT library. This library supports fourier transforms of float32 and float64 (i.e. single and double precision) tensors for all input sizes. For float16 (i.e. half precision) and bfloat16 inputs however, the dimensions which are transformed are restricted to powers of two. Since data is converted to one of these reduced precision floating point formats when torch.autocast is used, torch-harmonics will issue an error when the input shapes are not powers of two. For these cases, we recommend disabling autocast for the harmonics transform specifically:

import torch
import torch_harmonics as th

sht = th.RealSHT(512, 1024, grid="equiangular").cuda()

with torch.autocast(device_type="cuda", enabled = True):
   # do some AMP converted math here
   x = some_math(x)
   # convert tensor to float32
   x = x.to(torch.float32)
   # now disable autocast specifically for the transform,
   # making sure that the tensors are not converted
   # back to reduced precision internally
   with torch.autocast(device_type="cuda", enabled = False):
      xt = sht(x)

   # continue operating on the transformed tensor
   xt = some_more_math(xt)

Depending on the problem, it might be beneficial to upcast data to float64 instead of float32 precision for numerical stability.

Contributors

Boris Bonev ([email protected]), Thorsten Kurth ([email protected]), Mauro Bisson , Massimiliano Fatica, Nikola Kovachki, Jean Kossaifi, Christian Hundt

Cite us

If you use torch-harmonics in an academic paper, please cite [1]

@misc{bonev2023spherical,
      title={Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere},
      author={Boris Bonev and Thorsten Kurth and Christian Hundt and Jaideep Pathak and Maximilian Baust and Karthik Kashinath and Anima Anandkumar},
      year={2023},
      eprint={2306.03838},
      archivePrefix={arXiv},
      primaryClass={cs.LG}
}

References

[1] Bonev B., Kurth T., Hundt C., Pathak, J., Baust M., Kashinath K., Anandkumar A.; Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere; arXiv 2306.0383, 2023.

[2] Schaeffer N.; Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations; G3: Geochemistry, Geophysics, Geosystems, 2013.

[3] Wang B., Wang L., Xie Z.; Accurate calculation of spherical and vector spherical harmonic expansions via spectral element grids; Adv Comput Math, 2018.

[4] Ocampo, Price, McEwen, Scalable and equivariant spherical CNNs by discrete-continuous (DISCO) convolutions, ICLR (2023), arXiv:2209.13603