백트래킹은 해를 찾는 도중에 해가 아니어서 막히게 되면, BACK! 되돌아가서 다시 해를 찾아가는 기법을 말합니다.
- 해가 되지 않으면 그 경로는 쳐내게 되는데, 즉 가지치기 하게 되는데 이렇게 불필요한 경로를 쳐내기 때문에 효율적으로 문제를 처리할 수 있게 됩니다! (그만큼 가지치기를 잘해야겠죠..?)
- 백트래킹은 DFS(깊이 우선 탐색)를 기반으로 만들어집니다. DFS로 인해 해당 경우의 수로 탐색하며 내려가다가 해당 노드가 조건에 맞지 않는다고 생각되면 가지치기 하듯이 그 경우를 잘라내고 다시 상위 노드로 돌아가 다른 하위 노드로 내려가는 과정을 반복합니다.
- 백트래킹으로 문제를 풀 때 DFS로 모든 경우의 수를 탐색하다가 조건문을 걸어서 해가 절대로 될 수 없는 상황을 정의해주고, 그런 상황일 경우에는 탐색을 중지하고 그 이전으로 돌아가 다시 다른 경우를 탐색하게끔 구현할 수 있습니다.
다른 분들은 잘 알 것 같기는 한데.. 저는 잘 몰라서... 예.. 정리를 살짝만 해보자면~
💜 DFS(Depth First Search) 깊이 우선 탐색은 정점의 자식들을 먼저 탐색하는 방식입니다.
- DFS는 한 개의 큐와 한 개의 스택을 사용합니다.
- BFS보다 속도가 느릴 수 있습니다.
- 미로 게임 등에서 처럼 경로가 존재하는지 판별할 때 유용합니다.
읭? 뭔말이지? 아래 사진 한번 보고 가실게요~
-
BFS 방식: A - B - C - D - G - H - I - E - F - J
-
DFS 방식: A - B - D - E - F - C - G - H - I - J
-
DFS는 보시는 것 처럼 루트 노드 혹은 어떤 특정 노드에서 시작하여 해당 분기를 모두 검색하고 다음 분기로 넘어가는 방식입니다.
-
모든 노드를 방문하고 싶을 때 이 알고리즘을 사용하며 너비 우선 탐색(BFS)에 비해서 속도는 느리지만 구현이 조금 더 간결하다고 하네요!
-
재귀 구조를 가지고 자료구조 중 스택과 유사합니다. 재귀 구조를 가지기 때문에 알고리즘을 구현할 때 어느 정점을 방문했는지 꼭 체크가 필요하다고 합니당!! (넓게 찾기 전에 깊게 찾는다. 미로찾기와 비슷..)
....
오늘의 주제로 다시 돌아와서~다시 정리 한번 해보자면!
DFS
- DFS는 가능한 모든 경로를 탐색합니다!
- 그래서 불필요할 것 같은 경로를 사전에 차단하거나 하는 등의 행동이 없으므로 경우의 수를 줄이지 못합니다.
- 따라서~ N! 가지의 경우의 수를 가진 문제는 DFS로 처리가 불가능할 것입니다.
Backtracking
- 백트래킹은 해를 찾아가는 도중, 지금의 경로가 해가 될 것 같지 않으면 그 경로를 더 이상 가지 않고 되돌아갑니다.
- 코드로 치면 반복문의 횟수까지 줄일 수 있으므로 효율적입니다.
- 이를 가지치기라고 하는데, 불필요한 부분을 쳐내고 최대한 올바른 쪽으로 간다는 의미입니다.
- 일반적으로 불필요한 경로를 조기에 차단할 수 있게 되어서 경우의 수가 줄어들지만, 만약 N!의 경우의 수를 가진 문제에서 최악의 경우는 여전히 지수함수 시간을 필요로 하므로 처리가 불가능할 수 도 있습니다. 가지치기를 얼마나 잘하느냐에 따라 효율성이 결정되게 됩니다.
백트래킹은 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 것입니다. 즉, 답이 될만한지 판단하고 그렇지 않으면 그 부분까지 탐색하는 것을 하지 않고 가지치기 하는 것을 백트래킹이라고 생각하면 됩니다.
주로 문제 풀이에서는 DFS 등으로 모든 경우의 수를 탐색하는 과정에서, 조건문 등을 걸어 답이 절대로 될 수 없는 상황을 정의하고, 그러한 상황일 경우에는 탐색을 중지시킨 뒤 그 이전으로 돌아가서 다시 다른 경우를 탐색하게끔 구현할 수 있습니다.
어떤 노드의 유망성, 즉 해가 될 만한지 판단한 후 유망하지 않다고 결정되면 그 노드의 이전(부모)로 돌아가(Backtracking) 다음 자식 노드로 갑니다.
해가 될 가능성이 있으면 유망하다(promising)고 하며, 유망하지 않은 노드에 가지 않는 것을 가지치기(pruning)한다고 하는 것입니다.
만약 정렬되어 있지 않는 숫자 배열에서 특정 숫자를 찾아야 하는 경우는 0(n)의 시간 복잡도를 가집니다. 이 경우에서는 하나씩 살펴볼 수 밖에 없으므로 백트래킹을 적용할 수 없습니다!
백트래킹의 가장 대표적인 예시가 바로 N-Queen 문제입니다!
N-Queen 문제는 N개의 체스 퀸을 NxN 크기의 체스보드에서 움직이되, 상호 공격을 하지 않도록 움직이는 방법입니다.
한 행당 하나의 퀸만 들어가므로, 행당 한번 퀸이 어떤 위치에 올릴지 선택합니다.
만약 대각선 방향과 열방향으로 퀸이 존재한다면 해당 탐색은 멈추고, 이전 탐색으로 되돌아가서 진행합니다.
따라서 모든 경우를 탐색하는 방법보다 효율성이 좋습니다!
즉 정리하면~
- DFS를 통해 행당 하나의 퀸을 올린다. 행당 퀸이 올라간 열의 정보는
queens배열에 저장한다. 올리기 전에 올라갈 수 있는지 확인해야 한다. - isValid함수로 대각선, 열에 퀸이 존재하는지 확인한다. 존재한다면 해당 탐색을 더이상 진행하지 않는다. 이전 탐색으로 돌아가서 탐색을 진행한다.
queens의 길이가 N이라면 해당 탐색은 종료한다.queensPos배열에queens배열을 저장하고, 이전 탐색으로 돌아가서 탐색을 진행한다.
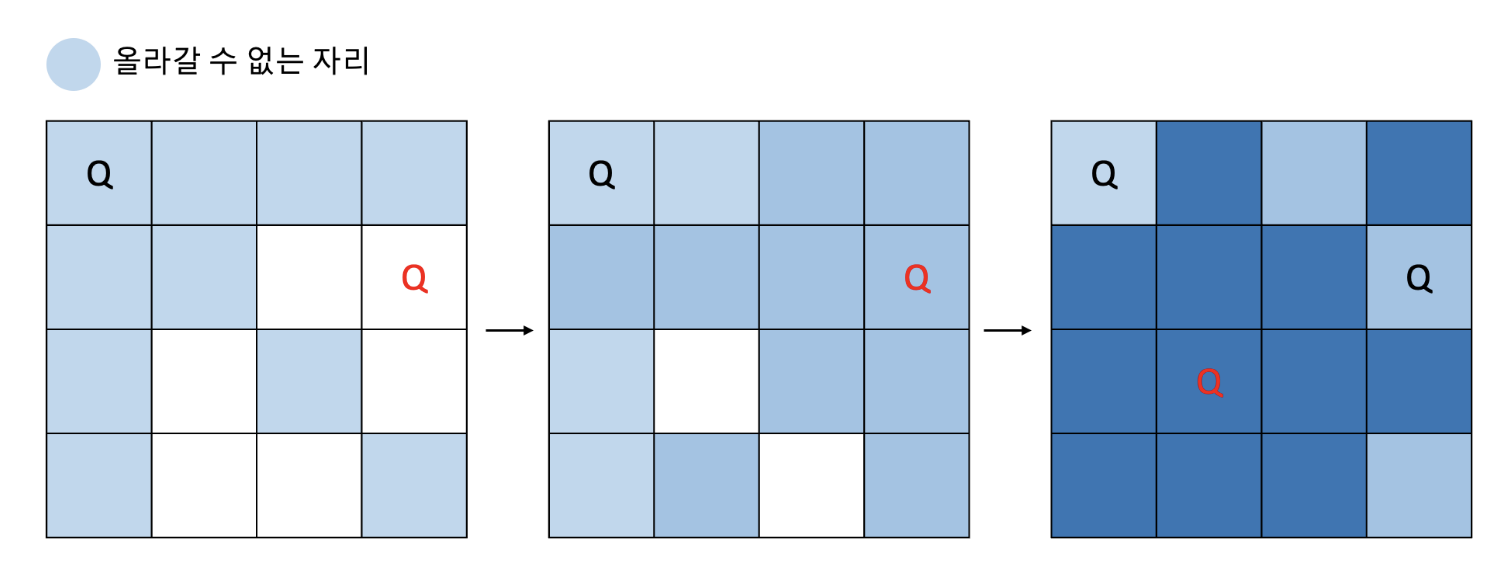
4X4 체스판에서 (0,0)에 퀸을 올릴 경우 흰색 칸에 다른 퀸을 올릴 수 있습니다.
만약 아래와 같이 (1,2)에 퀸을 올리면 퀸이 올라갈 수 있는 자리는 하나만 남게 되고, 4개를 올릴 수 없으므로 탐색을 종료하고 이전 탐색 단계로 진행합니다.
(1,3)에 퀸을 올리면 퀸을 아래와 같이 3개만 올릴 수 있습니다. 4개를 올릴 수 없으므로 탐색을 종료하고 이전 탐색 단계를 진행합니다.
이런식으로 탐색을 진행하다 보면 4X4 체스판에서는 다음과 같은 경우가 답이 됩니다.
const solveNQueens = n => {
const board = Array(n)
.fill()
.map(() => Array(n).fill(0));
const queensPos = [];
const queens = [];
// 대각선, 열에 퀸이 존재하지 않는다면 탐색을 진행함
const DFS = L => {
if (queens.length === n) {
queensPos.push(queens.slice());
return;
} else {
// 행당 하나의 퀸만 올라감
for (let i = 0; i < n; i++) {
if (isValid(L, i)) {
board[L][i] = 1;
queens.push(i);
DFS(L + 1);
board[L][i] = 0;
queens.pop();
}
}
}
};
// 대각선, 열에 퀸이 존재하는지 확인함
const isValid = (x, y) => {
// 같은 열에 퀸 존재하는지 확인
for (let i = 0; i < x; i++) {
if (board[i][y]) return false;
}
// \ 대각선에 퀸 존재하는지 확인
for (let i = 1; ; i++) {
if (x - i < 0 || y - i < 0) break;
if (board[x - i][y - i]) return false;
}
// / 대각선에 퀸 존재하는지 확인
for (let i = 1; ; i++) {
if (x - i < 0 || y + i >= n) break;
if (board[x - i][y + i]) return false;
}
return true;
};
const createStringAnswer = () => {
const answer = [];
for (const queens of queensPos) {
const temp = [];
for (const pos of queens) {
const str = '.'.repeat(pos) + 'Q' + '.'.repeat(n - pos - 1);
temp.push(str);
}
answer.push(temp);
}
return answer;
};
DFS(0);
return createStringAnswer();
};N-Queen 해설?영상