GPU Mandelbrot

The mandelbrot fractal is really interesting, and also very simple to implement so it's a nice starter project

---

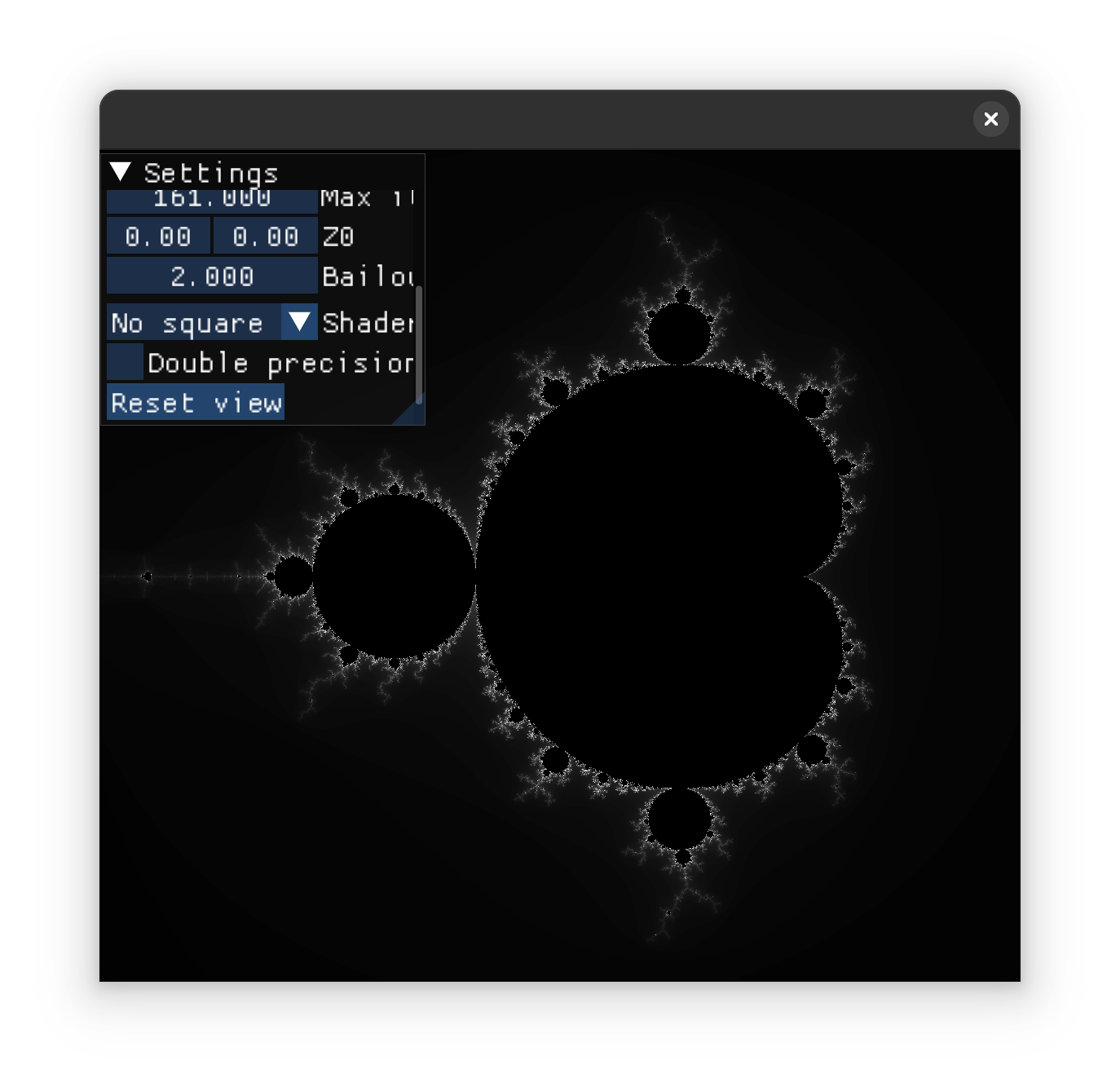
It's a learning project for dear-imgui, opengl and c++, with the goal of implementing various mandelbrot algorithms, and julia sets in the future.

Robert Munafo's https://www.mrob.com/pub/muency.html blog is full of tips and information on implementing mandelbrot algorithms and was of great help.

---

Pictures

Traditional iterated algorithm:

This algorithm computes the time needed for a complex number $z$ to escape to infinity with:
$z_0 = 0$
$z = z^2 + c$
Here, $c$ is the coordinates of the point in the complex plane, aka the pixel on screen.

Any point $z$ with $|z| > 2$ will escape to infinity, so the condition for the main loop looks something like this: while(mag(z) <= 2 && iter < max_iter)

Derivative bailout

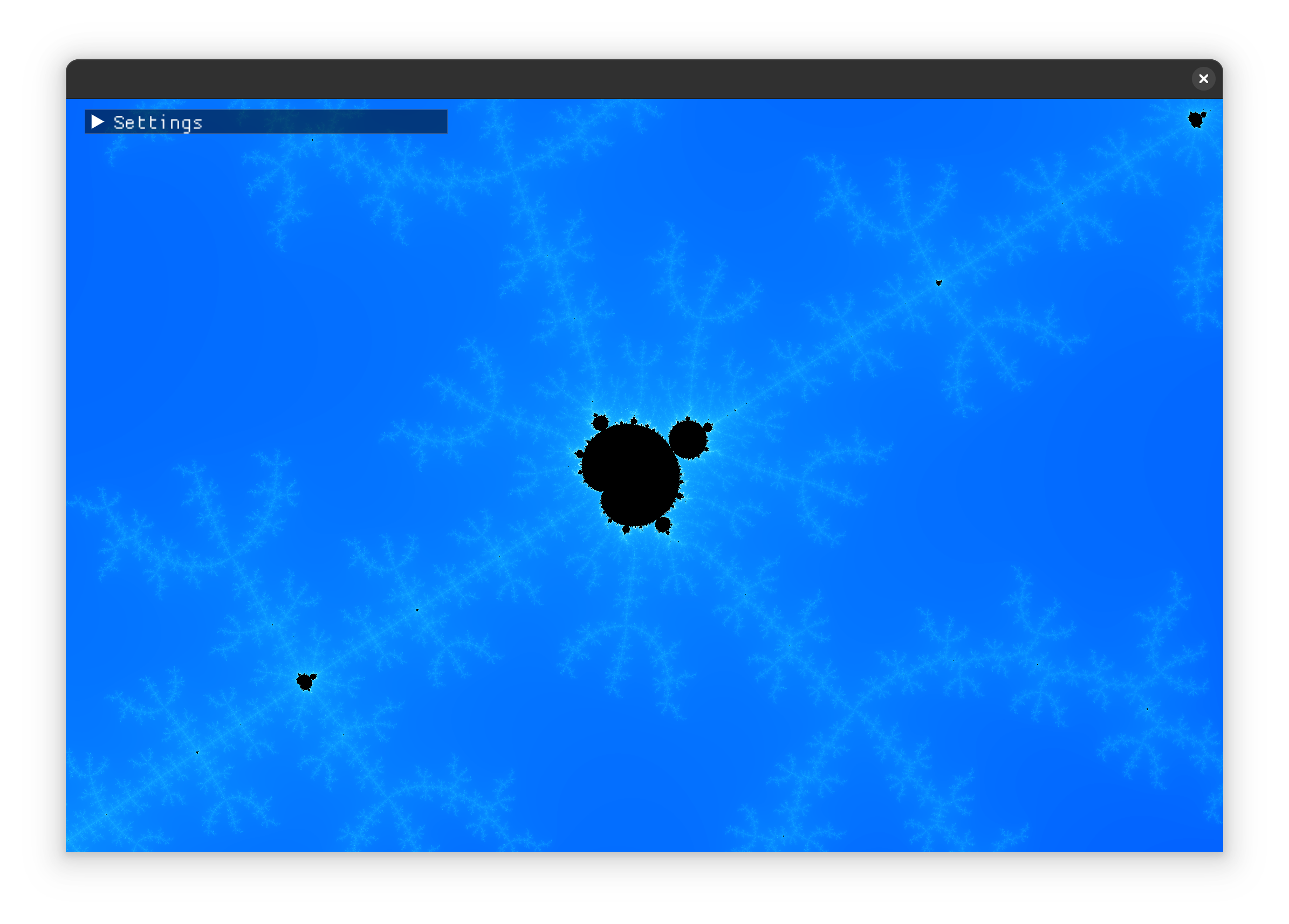
This algorithm is less known, by me too as it was my first time implementing it. It checks if the sum of the derivatives is bigger than a given value, in which case it stops.
This algorithm has the benefit of showing some structures inside the bulbs
According to wikipedia, the derivative $z^\prime_n$ at $z_n$, with $n$ the iteration number, is given by:
$z^\prime_n = 2*z^\prime_{n-1}*z_{n-1}+1$

Wikipedia also gave a python sample which I translated in glsl for my first attempt at implementing it in fs_derivative.glsl:

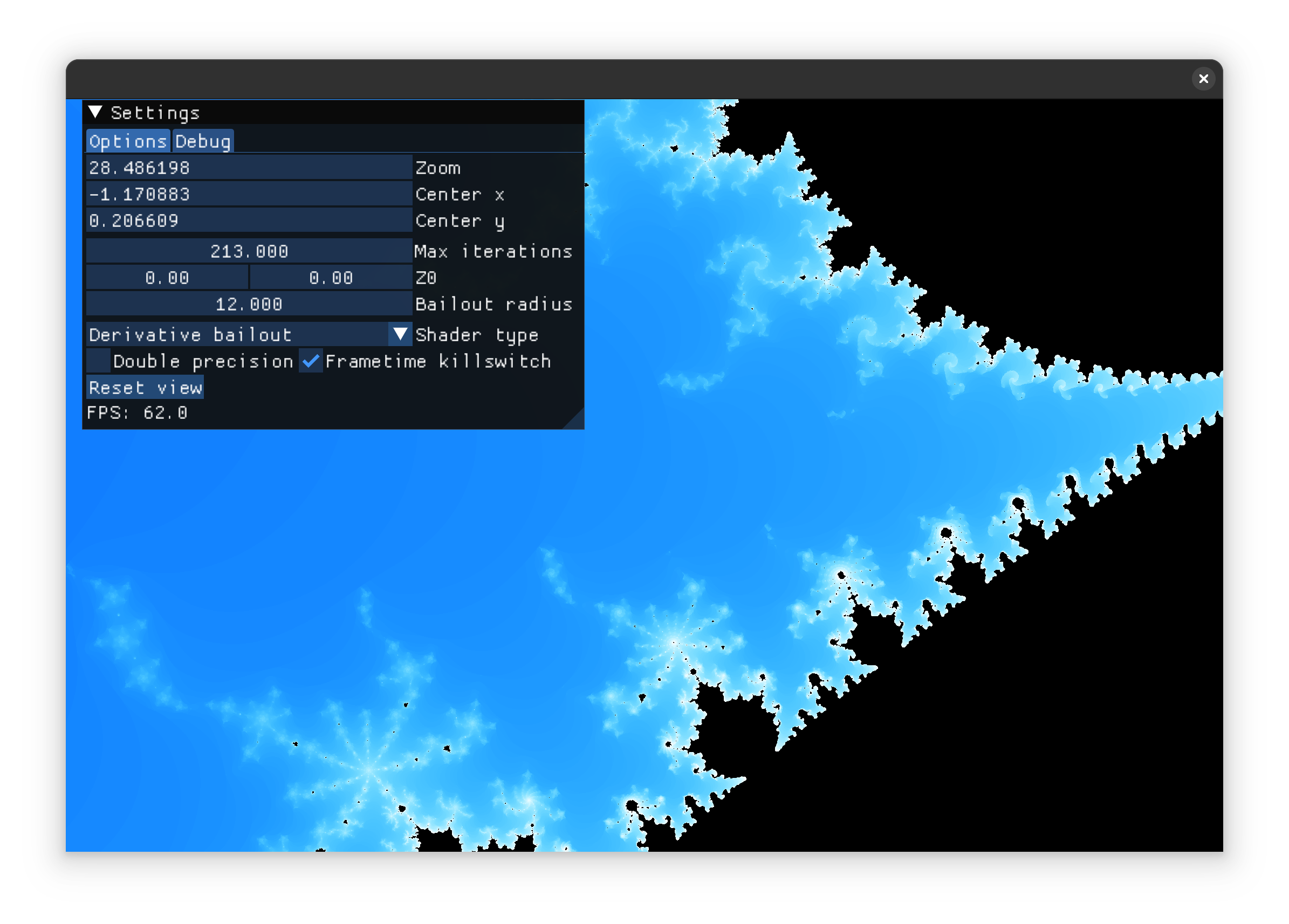
My second attempt in fs_derivative_2.glsl used the definition, and with a few tweaks for the coloring, seems to give satisfying results:

Continuous coloring

Because the iteration count is an integer, at low iteration counts, some color bands are very visible and does not natively allow for smooth transitions between one iteration to the other.

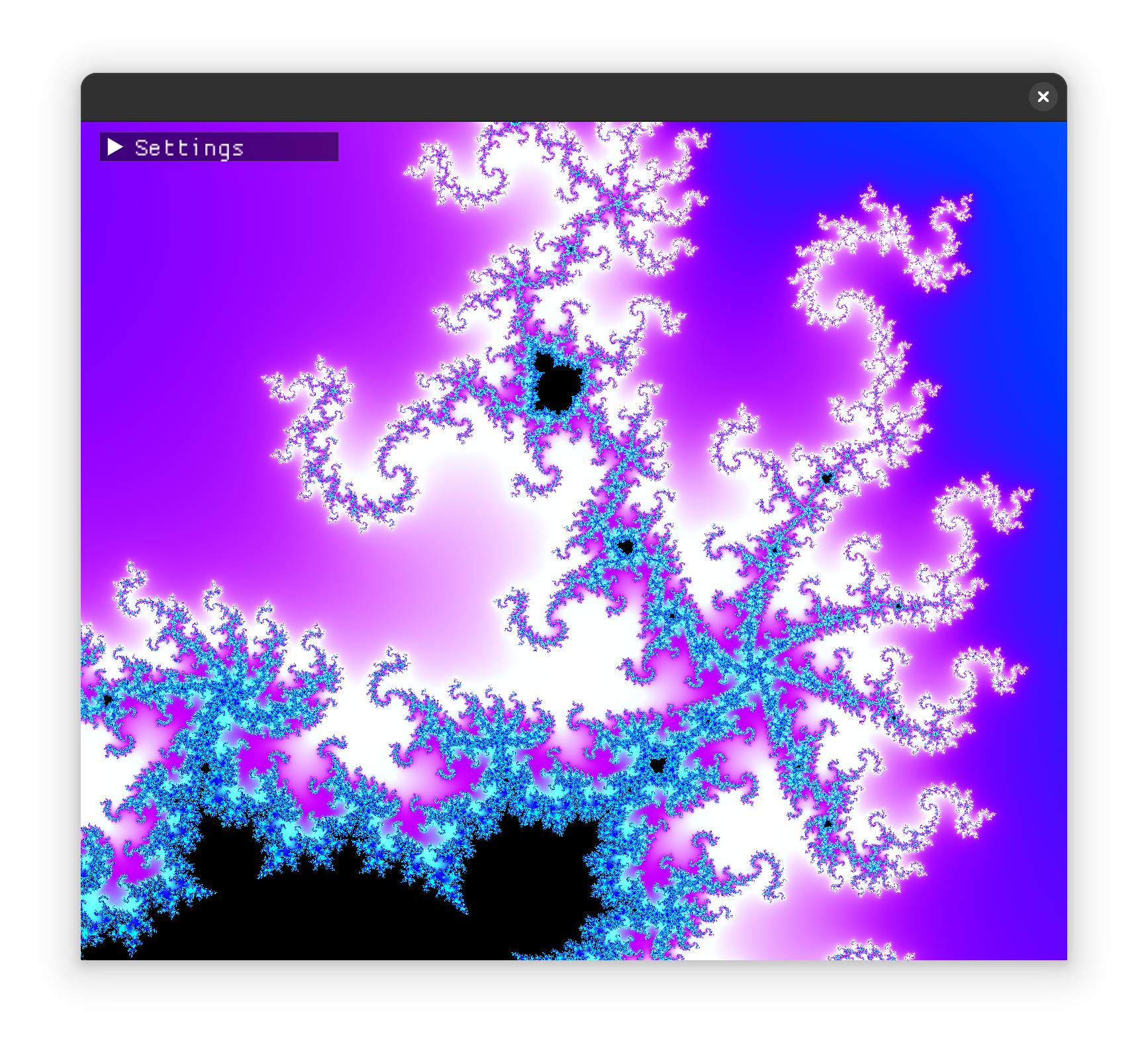
From Robert Munafo's website, after computing the final iteration count $n$, a smooth gradient can be obtained by adding some biais $b \in [0, 1]$ to $n$, with:
$b = 1+log_2(log_2(r))-log_2(log_2(|z_n|))$
$r$ being the bailout radius, and $z_n$ the final iterated number at time of bailout.

The final results are a nice smooth gradient:

---

This code is under the MIT License