Non-Stochastic-Bandit-Slate-Algorithms

Introduction

Implementations of the bandit algorithms with unordered and ordered slates that are described in the paper "Non-Stochastic Bandit Slate Problems", by Kale et al. 2010.

We consider bandit problems, motivated by applications in online advertising and news story selection, in which the learner must repeatedly select a slate, that is, a subset of size s from K possible actions, and then receives rewards for just the selected actions. The goal is to minimize the regret with respect to total reward of the best slate computed in hindsight.¹

In the unordered version of the problem, the reward to the learning algorithm is the sum of the rewards of the chosen actions in the slate. So the chosen actions all have a weight of 1 and therefore they are “unordered”.

In the ordered slate problem, the adversary specifies a reward for using an action in a specific position. The reward to the learner then is the sum of the rewards of the (actions, position) pairs in the chosen ordered slate.

Results

Sample plots that are obtained using the Environment class in TestEnvironment folder is given below.

-> For the unordered case, each arm was associated with a normal probability distribution with a mean between [-0.4, 0.4] and std = 0.3. The mean was selected at the start from a uniform random distribution from the range of [-0.4, 0.4].

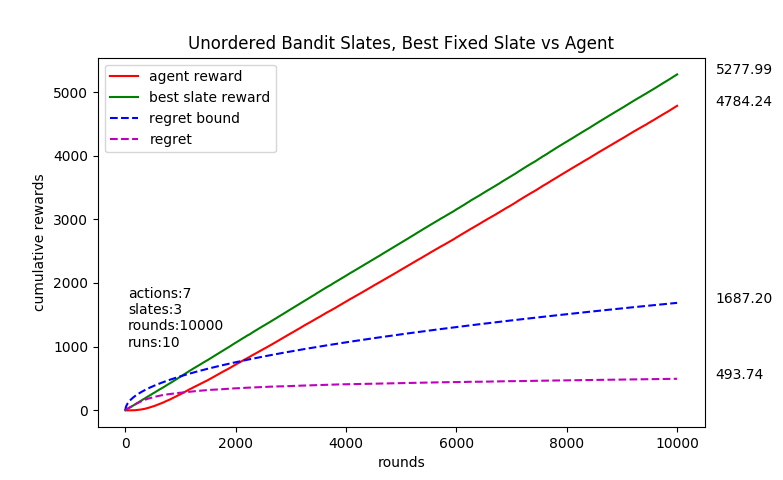
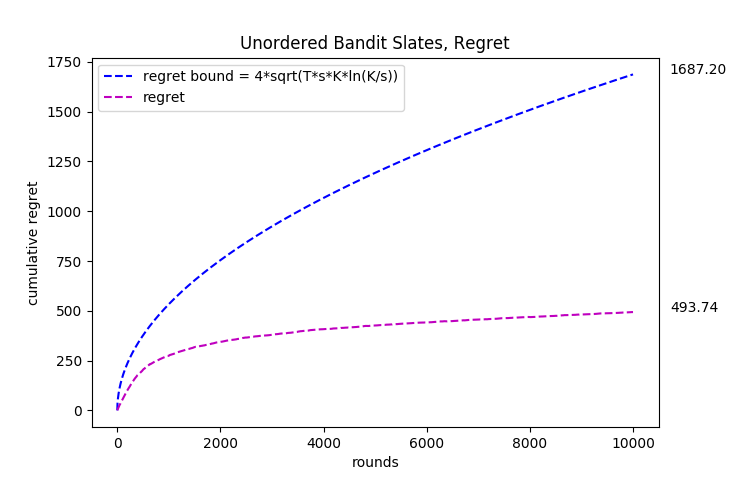
-> For the ordered case, each arm is again associated with a normal probability distribution with a mean between [-0.4, 0.4] and std = 0.3. The mean is selected at start from a uniform random distribution from the range of [-0.4, 0.4]. First action chosen has a multiplier of 1, second action chosen has a multiplier of 1.1, third has a multiplier of 1.2 and so on. Therefore successive positions have increasing importance.

Sample Code

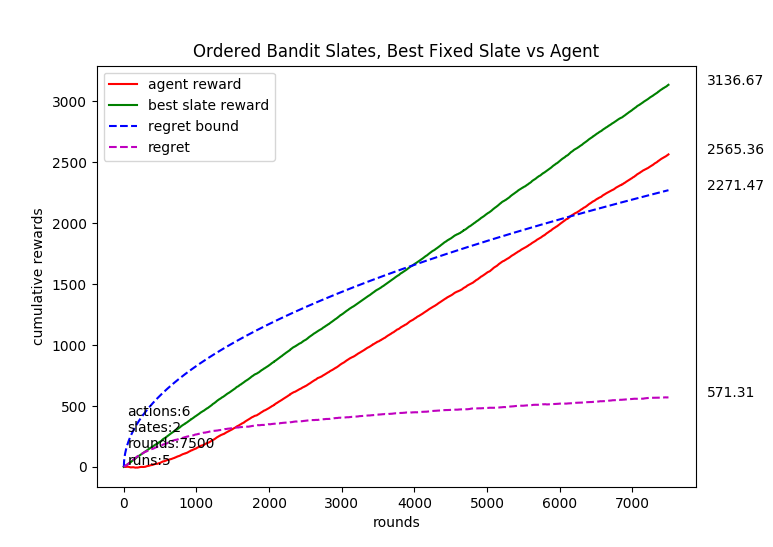
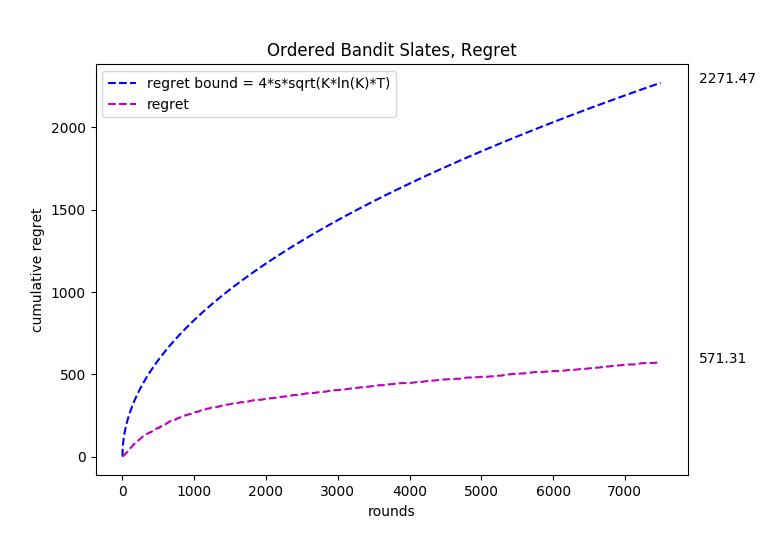
Sample code to run the bandit algorithms is given below. More can be found in the folder TestEnvironment.

import UnorderedSlatesBandit as unordered
import OrderedSlatesBandit as ordered
import numpy as np
import math

# use the bandit algo. with either the ordered or unordered slates.
agent = unordered.UnorderedSlatesBandit(actions, slate_size, rounds)
# agent = ordered.OrderedSlatesBandit(actions, slate_size, rounds)

# set up the environment function which will reward/punish the agent.
# environment function should take a slate indicator vector or slate-position subpermutation matrix as input
# and return a loss/reward vector/matrix of dimensions that equal input vector(size K) or input matrix(shape (s,K)).
agent.set_environment(environment.get_blind_loss)

# run the agent for 'rounds' times.
agent.iterate_agent()

# environment is responsible of storing best_fixed_slate_data. (losses are defined as positive numbers while all rewards
# are defined as negative, thus the minus sign before agent.loss_vs_rounds.)
print("\nagent total reward: {0} vs best fixed slate total reward: {1}".format(-np.sum(agent.loss_vs_rounds), -np.sum(environment.best_slate_vs_rounds)))

References

¹S. Kale, L. Reyzin, and R. Schapire. Non-Stochastic Bandit Slate Problems. Advances in Neural Information Processing Systems 23. 2010.