nadir (noun): nā-dir
the lowest point.
Fitting with the minimum loss based estimation12 literature,
{nadir} is an implementation of the super learner algorithm with
improved support for flexible formula based syntax and which is fond of
functional programming techniques such as closures, currying, and
function factories.
{nadir} implements the super learner algorithm3. To quote the
Guide to SuperLearner4 (a previous implementation):
SuperLearner is an algorithm that uses cross-validation to estimate the performance of multiple machine learning models, or the same model with different settings. It then creates an optimal weighted average of those models, aka an “ensemble”, using the test data performance. This approach has been proven to be asymptotically as accurate as the best possible prediction algorithm that is tested.
{nadir} is currently undergoing active development. Major features, such
as the super_learner() and cv_super_learner() function are
considered stable at this time. However, in the future the features
offered may be expanded.
In previous implementations
({SuperLearner},
{sl3},
{mlr3superlearner}),
support for flexible formula-based syntax has been limited, instead
opting for specifying learners as models on an lme4 and mgcv (for
random effects and generalized additive models) use formulas extensively
to specify models using syntax like (age | strata) to specify random
effects on age by strata, or s(age, income) to specify a smoothing
term on age and income simultaneously.
At present, it is difficult to use these kinds of features in
{SuperLearner}, {sl3} and {mlr3superlearner}.
For example, it is easy to imagine the super learner algorithm being appealing to modelers fond of random effects based models because they may want to hedge on the exact nature of the random effects models, not sure if random intercepts are enough or if random slopes should be included, etc., and similar other modeling decisions in other frameworks.
Therefore, the {nadir} package takes as its charges to:
- Implement a syntax in which it is easy to specify different formulas for each of many candidate learners.
- To make it easy to pass new learners to the Super Learner algorithm.
At present, {nadir} is only available on GitHub.
devtools::install_github("ctesta01/nadir")Warning: this package is currently under active development and may be wrong! Do not use this for serious applications until this message has been removed, likely at the time of a future release.
First, let’s start with the simplest possible use case of
nadir::super_learner(), which is where the user would like to feed in
data, a specification for some regression formula(s), specify a library
of learners, and get back a prediction function that is suitable for
plugging into downstream analyses, like in Targeted Learning or for
pure-prediction applications.
Here is a demo of an extremely simple application of using
nadir::super_learner:
library(nadir)
# we'll use a few basic learners
learners <- list(
glm = lnr_glm,
rf = lnr_rf,
glmnet = lnr_glmnet
)
# more learners are available, see ?learners
sl_model <- super_learner(
data = mtcars,
formula = mpg ~ cyl + hp + disp,
learners = learners)
# the output from super_learner is a prediction function:
# here we are producing predictions based on a weighted combination of the
# trained learners.
predict(sl_model, mtcars) |> head()## Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive
## 20.41648 20.41648 24.20135 19.85172
## Hornet Sportabout Valiant
## 16.89780 19.59764
Continuing with our mtcars example, suppose the user would really like
to use random effects or similar types of fancy formula language
features. One easy way to do so with nadir::super_learner is using the
following syntax:
learners <- list(
glm = lnr_glm,
rf = lnr_rf,
glmnet = lnr_glmnet,
lmer = lnr_lmer,
gam = lnr_gam
)
formulas <- c(
.default = mpg ~ cyl + hp + disp, # our first three learners use same formula
lmer = mpg ~ (1 | cyl) + hp + disp, # both lme4::lmer and mgcv::gam have
gam = mpg ~ s(hp) + cyl + disp # specialized formula syntax
)
# fit a super_learner
sl_model <- super_learner(
data = mtcars,
formulas = formulas,
learners = learners)
predict(sl_model, mtcars) |> head()## Mazda RX4 Mazda RX4 Wag Datsun 710 Hornet 4 Drive
## 20.53980 20.53980 24.43141 19.74459
## Hornet Sportabout Valiant
## 16.82782 19.64837
To put the learners and the super learner algorithm on a level playing field, it’s important that learners and super learner both be evaluated on held-out validation/test data that the algorithms have not seen before.
Using the output from nadir::super_learner(), we can call
compare_learners() to see the mean-squared-error (MSE) on the held-out
data, also called CV-MSE, for each of the candidate learners specified.
# construct our super learner and call compare_learners on it
sl_model <- super_learner(
data = mtcars,
formulas = formulas,
learners = learners)
compare_learners(sl_model)## Inferring the loss metric for learner comparison based on the outcome type:
## outcome_type=continuous -> using mean squared error
## # A tibble: 1 × 5
## glm rf glmnet lmer gam
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 10.8 7.25 10.9 9.44 10.9
Plotting code
pacman::p_load('dplyr', 'ggplot2', 'tidyr', 'magrittr')
truth <- sl_model$holdout_predictions$mpg
holdout_var <- sl_model$holdout_predictions |>
dplyr::group_by(.sl_fold) |>
dplyr::summarize(across(everything(), ~ mean((. - mpg)^2))) |>
dplyr::summarize(across(everything(), var)) |>
select(-mpg, -.sl_fold) |>
t() |>
as.data.frame() |>
tibble::rownames_to_column('learner') |>
dplyr::rename(var = V1) |>
dplyr::mutate(sd = sqrt(var))
jitters <- sl_model$holdout_predictions |>
dplyr::mutate(dplyr::across(-.sl_fold, ~ (. - mpg)^2)) |>
dplyr::select(-mpg) %>%
tidyr::pivot_longer(cols = 2:ncol(.), names_to = 'learner', values_to = 'squared_error') |>
dplyr::group_by(learner, .sl_fold) |>
dplyr::summarize(mse = mean(squared_error)) |>
ungroup() |>
rename(fold = .sl_fold)## `summarise()` has grouped output by 'learner'. You can override using the
## `.groups` argument.
learner_comparison_df <- sl_model |>
compare_learners() |>
t() |>
as.data.frame() |>
tibble::rownames_to_column(var = 'learner') |>
dplyr::mutate(learner = factor(learner)) |>
dplyr::rename(mse = V1) |>
dplyr::left_join(holdout_var) |>
dplyr::mutate(
upper_ci = mse + sd,
lower_ci = mse - sd) |>
dplyr::mutate(learner = forcats::fct_reorder(learner, mse))## Inferring the loss metric for learner comparison based on the outcome type:
## outcome_type=continuous -> using mean squared error
## Joining with `by = join_by(learner)`
jitters$learner <- factor(jitters$learner, levels = levels(learner_comparison_df$learner))
learner_comparison_df |>
ggplot2::ggplot(ggplot2::aes(y = learner, x = mse, fill = learner)) +
ggplot2::geom_col(alpha = 0.5) +
ggplot2::geom_jitter(data = jitters, mapping = ggplot2::aes(x = mse), height = .15, shape = 'o') +
ggplot2::geom_pointrange(mapping = ggplot2::aes(xmax = upper_ci, xmin = lower_ci),
alpha = 0.5) +
ggplot2::theme_bw() +
ggplot2::ggtitle("Comparison of Candidate Learners") +
ggplot2::labs(caption = "Error bars show ±1 standard deviation across the CV estimated MSE for each learner\n
Each open circle represents the hold-out MSE of one fold of the data") +
ggplot2::theme(plot.caption.position = 'plot')
Now how should we go about getting the CV-MSE from a super learned
model? We will use the cv_super_learner() function that performs
another layer of cross-validation in order to assess the specified super
learner on folds of held-out data.
If you’d like to read more about how the internals of
cv_super_learner() work, please refer to the article Currying,
Closures, and Function
Factories
article
cv_results <- cv_super_learner(
data = mtcars,
formulas = formulas,
learners = learners)
cv_results## $cv_trained_learners
## # A tibble: 5 × 4
## split learned_predictor predictions mpg
## <int> <list> <list> <list>
## 1 1 <fn> <dbl [6]> <dbl [6]>
## 2 2 <fn> <dbl [7]> <dbl [7]>
## 3 3 <fn> <dbl [6]> <dbl [6]>
## 4 4 <fn> <dbl [6]> <dbl [6]>
## 5 5 <fn> <dbl [7]> <dbl [7]>
##
## $cv_loss
## [1] 7.337934
Plotting code
cv_jitters <- cv_results$cv_trained_learners |>
dplyr::select(split, predictions, mpg) |>
tidyr::unnest(cols = c('predictions', 'mpg')) |>
dplyr::group_by(split) |>
dplyr::summarize(mse = mean((mpg - predictions)^2)) |>
dplyr::bind_cols(learner = 'super_learner')
cv_var <- cv_results$cv_trained_learners |>
dplyr::select(split, predictions, mpg) |>
tidyr::unnest(cols = c(predictions, mpg)) |>
dplyr::mutate(squared_error = (mpg - predictions)^2) |>
dplyr::group_by(split) |>
dplyr::summarize(mse = mean(squared_error)) |>
dplyr::summarize(
var = var(mse),
mse = mean(mse),
sd = sqrt(var),
upper_ci = mse + sd,
lower_ci = mse - sd) |>
dplyr::bind_cols(learner = 'super_learner')
new_jitters <- bind_rows(jitters, cv_jitters)
learner_comparison_df |>
bind_rows(cv_var) |>
dplyr::mutate(learner = forcats::fct_reorder(learner, mse)) |>
ggplot2::ggplot(ggplot2::aes(y = learner, x = mse, fill = learner)) +
ggplot2::geom_col(alpha = 0.5) +
ggplot2::geom_jitter(data = new_jitters, mapping = ggplot2::aes(x = mse), height = .15, shape = 'o') +
ggplot2::geom_pointrange(mapping = ggplot2::aes(xmax = upper_ci, xmin = lower_ci),
alpha = 0.5) +
ggplot2::theme_bw() +
ggplot2::scale_fill_brewer(palette = 'Set2') +
ggplot2::ggtitle("Comparison of Candidate Learners against Super Learner") +
ggplot2::labs(caption = "Error bars show ±1 standard deviation across the CV estimated MSE for each learner\n
Each open circle represents the hold-out MSE of one fold of the data") +
ggplot2::theme(plot.caption.position = 'plot')
Model hyperparameters are easy to handle in {nadir}. Two easy
solutions are available to users:
nadir::super_learner()has anextra_learner_argsparameter that can be passed a list of extra arguments for each learner.- Users can always build new learners (which allows for building in the
hyperparameter specification), and using the
...syntax, it’s easy to build new learners from the learners already provided by{nadir}.
Here’s some examples showing each approach.
# when using extra_learner_args, it's totally okay to use the
# same learner multiple times as long as their hyperparameters differ.
sl_model <- nadir::super_learner(
data = mtcars,
formula = mpg ~ .,
learners = c(
glmnet0 = lnr_glmnet,
glmnet1 = lnr_glmnet,
glmnet2 = lnr_glmnet,
rf0 = lnr_rf,
rf1 = lnr_rf,
rf2 = lnr_rf
),
extra_learner_args = list(
glmnet0 = list(lambda = 0.01),
glmnet1 = list(lambda = 0.1),
glmnet2 = list(lambda = 1),
rf0 = list(ntree = 3),
rf1 = list(ntree = 10),
rf2 = list(ntree = 30)
)
)
compare_learners(sl_model)## Inferring the loss metric for learner comparison based on the outcome type:
## outcome_type=continuous -> using mean squared error
## # A tibble: 1 × 6
## glmnet0 glmnet1 glmnet2 rf0 rf1 rf2
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.000137 0.0137 1.37 10.1 7.00 5.77
When does it make more sense to build new learners with the
hyperparameters built into them rather than using the
extra_learner_args parameter?
One instance when building new learners may make sense is when the user
would like to produce a large number of hyperparameterized learners
programmatically, for example over a grid of hyperparameter values.
Below we show such an example for a 1-d grid of hyperparameters with
glmnet.
# produce a "grid" of glmnet learners with lambda set to
# exp(-1 to 1 in steps of .1)
hyperparameterized_learners <- lapply(
exp(seq(-1, 1, by = .1)),
function(lambda) {
# create a new learner with given lambda
new_learner <- function(data, formula, ...) {
lnr_glmnet(data, formula, lambda = lambda, ...) }
# declare it to be a continuous outcome learner
attr(new_learner, 'sl_lnr_type') <- 'continuous'
return(new_learner)
}
)
# give them names because nadir::super_learner requires that the
# learners argument be named.
names(hyperparameterized_learners) <- paste0('glmnet', 1:length(hyperparameterized_learners))
# fit the super_learner with 20 glmnets with different lambdas
sl_model_glmnet <- nadir::super_learner(
data = mtcars,
learners = hyperparameterized_learners,
formula = mpg ~ .)
compare_learners(sl_model_glmnet)## Inferring the loss metric for learner comparison based on the outcome type:
## outcome_type=continuous -> using mean squared error
## # A tibble: 1 × 21
## glmnet1 glmnet2 glmnet3 glmnet4 glmnet5 glmnet6 glmnet7 glmnet8 glmnet9
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 0.146 0.178 0.217 0.265 0.324 0.396 0.483 0.590 0.721
## # ℹ 12 more variables: glmnet10 <dbl>, glmnet11 <dbl>, glmnet12 <dbl>,
## # glmnet13 <dbl>, glmnet14 <dbl>, glmnet15 <dbl>, glmnet16 <dbl>,
## # glmnet17 <dbl>, glmnet18 <dbl>, glmnet19 <dbl>, glmnet20 <dbl>,
## # glmnet21 <dbl>
R is a functional programming language, which allows for functions to
build and return functions just like any other return object.
We refer to functions that create and return another function as a function factory. For an extended reference, see the Advanced R book.
Function factories are so useful in {nadir} because, at their essence,
a candidate learner needs to be able to 1) accept training data, and 2)
produce a prediction function that can make predictions on heldout
validation data. So a typical learner in {nadir} looks like:
lnr_lm <- function(data, formula, ...) {
model <- stats::lm(formula = formula, data = data, ...)
predict_from_trained_lm <- function(newdata) {
predict(model, newdata = newdata, type = 'response')
}
return(predict_from_trained_lm)
}Moreover, given how code-lightweight it is to write a simple learner, this makes it relatively easy for users to write new learners that meet their exact needs.
If you want to implement your own learners, you just need to follow the following pseudocode approach:
lnr_custom <- function(data, formula, ...) {
model <- # train your model using data, formula, ...
predict_from_model <- function(newdata) {
return(...) # return predictions from the trained model
# (predictions should be a vector of predictions, one for each row of newdata)
}
return(predict_from_model)
}For more details, read the Currying, Closures, and Function Factories article
There is built-in support for
- Binary and multiclass outcomes
- Density estimation
- Using observation weights
- Running
super_learner()in parallel - Graceful error handling
- Survival analysis via pooled logistic regression
- Working with clusters and strata
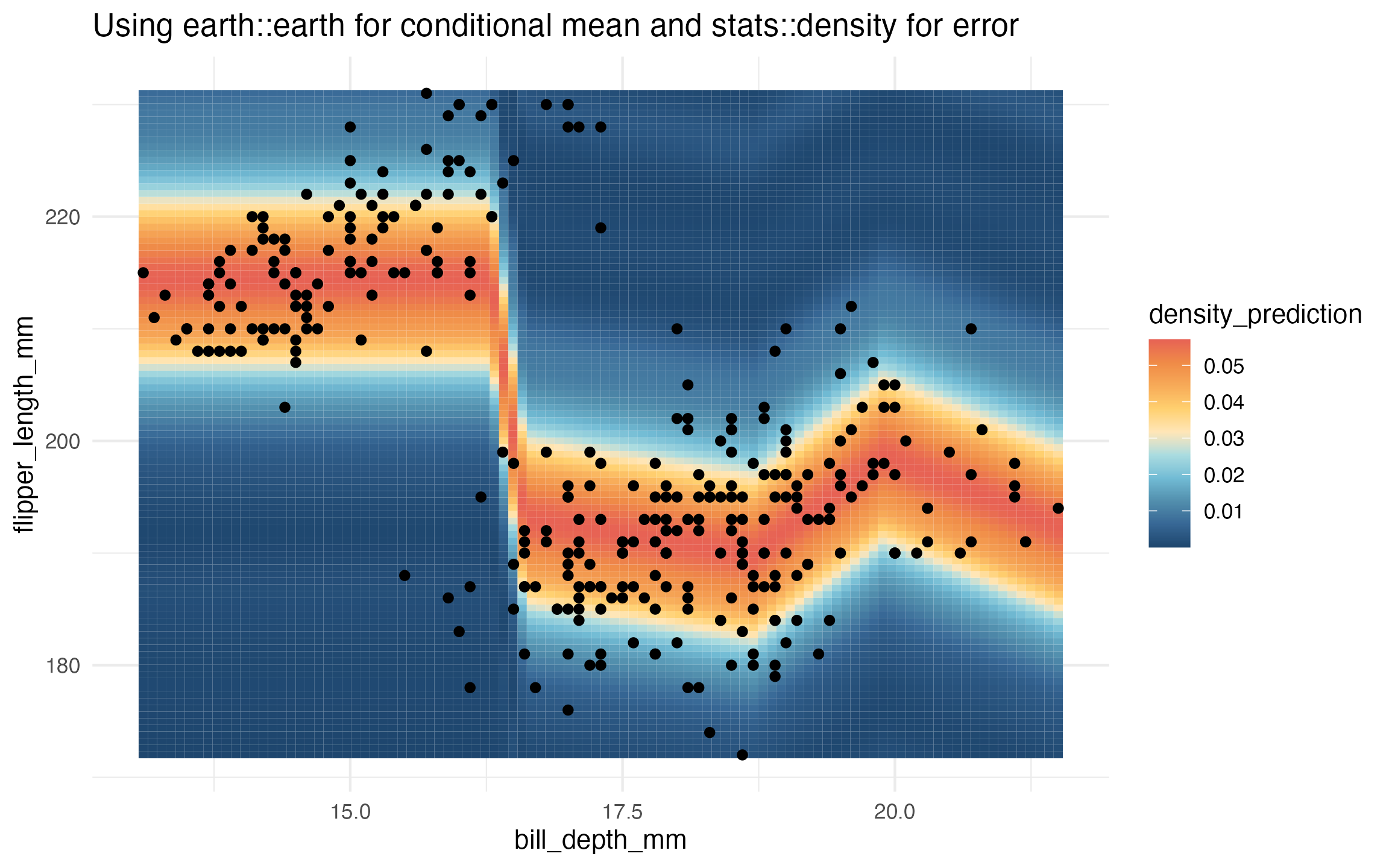
As a teaser, here’s an example visualization of a density learner
trained on the penguins data:
We also have ≥34 tests (and counting!) that are run at every update to ensure the correctness of the implementation.
View the source code for the tests that are part of {nadir}:
Check out the complete documentation on the package website:
- (Even More) Automated tests that try to ensure validity/correctness of the implementation!
- More built-in learners (incl. gradient boosted machines, polspline, etc.)
- We may extend to time-series and more outcome types in the future!
Footnotes
-
van der Laan, Mark J. and Dudoit, Sandrine, “Unified Cross-Validation Methodology For Selection Among Estimators and a General Cross-Validated Adaptive Epsilon-Net Estimator: Finite Sample Oracle Inequalities and Examples” (November 2003). U.C. Berkeley Division of Biostatistics Working Paper Series. Working Paper 130. https://biostats.bepress.com/ucbbiostat/paper130/ ↩
-
Zheng, W., & van der Laan, M. J. (2011). Cross-Validated Targeted Minimum-Loss-Based Estimation. In Springer Series in Statistics (pp. 459–474). Springer New York. https://doi.org/10.1007/978-1-4419-9782-1_27 ↩
-
van der Laan, M. J., Polley, E. C., & Hubbard, A. E. (2007). Super Learner. In Statistical Applications in Genetics and Molecular Biology (Vol. 6, Issue 1). Walter de Gruyter GmbH. https://doi.org/10.2202/1544-6115.1309 https://pubmed.ncbi.nlm.nih.gov/17910531/ ↩
-
Guide to
{SuperLearner}: https://cran.r-project.org/package=SuperLearner ↩