Assignment 4

Due date: 21 May, 2017.

Mathematical Expressions, Automatic Differentiation and Algebraic Simplification

In this assignment we will put aside our game for a little while, and delve instead into the magical world of mathematics. We will implement a system that can represent nested mathematical expressions that include variables, evaluate their values for specific variable assignments, differentiate them, and simplify the results.

In doing so we will work in a recursive framework, see some more examples of polymorphism, and practice the use of inheritance and class hierarchies for sharing of common code.

Part 1 -- Mathematical Expressions

Introduction:

Our goal is to represent mathematical expressions such as:

sin(((2x + y) * 4)^x)

Where the ^ symbol denotes the "power" operator, and x and y are variables.

Note that this somewhat complicated expression is composed of atomic expressions which are either binary or unary, arranged in a tree structure. The expression itself is the root of the tree.

The unary expressions are:

• Var("x") indicating that x is a variable.
• Sin(x) indicating the sinus of the value of x.

The binary expressions are:

• Plus(x,y) indicating the addition of x and y
• Mul(x,y) indicating the multiplication of x and y
• Pow(x,y) indicating raising x to the y power.

We also have a Num(4) expression indicating the number 4.

Assuming we represent each of the atomic expressions as a Class of the same name that take its arguments in the constructor, we can create the expression above in java using:

Expression e = new Sin(
                     new Pow(
                        new Mul(
                           new Plus(
                              new Mul(new Num(2), new Var("x")),
                              new Var("y")),
                           new Num(4)),
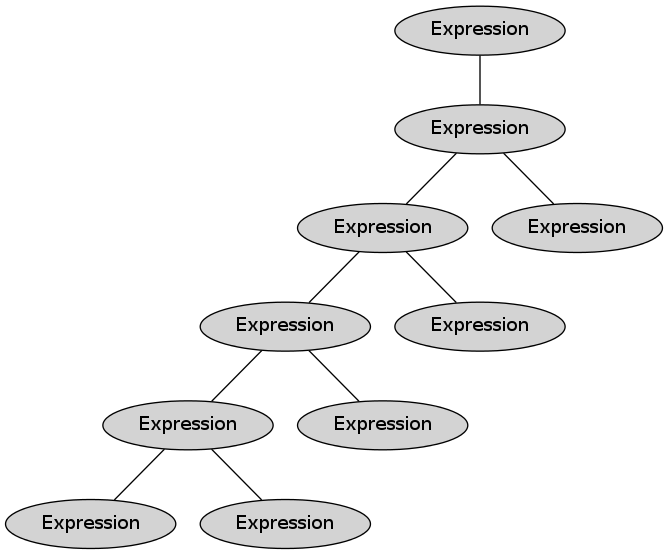
                     new Var("x")))

The tree is given below:

Note that all the nodes in the tree are expressions (according to the Expression interface):

Similarly, we could represent (x + y)^2 as:

Expression e2 = new Pow(new Plus(new Var("x"), new Var("y")), new Num(2));

Once we have an expression, we would like to be able to:

• Get a nice and readable string representation:

  String s = e2.toString();
  System.out.println(s);

  Should print ((x + y)^2)

• Ask about the variables in the expression: (this example uses generics)

  List<String> vars = e2.getVariables();
  for (String v : vars) {
     System.out.println(v);
  }   

  Should print

  x
  y
  

• Assign values to variables:

  Expression e3 = e2.assign("y", e2);
  System.out.println(e3);
  // (x + ((x + y)^2))^2
  e3 = e3.assign("x", new Num(1))
  System.out.println(e3);
  // (1 + ((1 + y)^2))^2

  In the first assign the variable y was assigned the Expression (x+y)^2, while in the second assign the variable x was assigned the Expression 1.

• Evaluate its value for a given variable assignment to numbers: (this example uses a mapping)

  Map<String, Double> assignment = new TreeMap<String, Double>();
  assignment.put("x", 2);
  assignment.put("y", 4);
  double value = e2.evaluate(assignment);
  System.out.println("The result is: " + value);

  Should print The result is: 36

  In this last example, we make use of the Map interface for mapping keys to values. We created a map called assignment mapping the value "x" to 2 and the value "y" to 4, and then evaluated the expression e2 with these values, resulting in (2 + 4)^2, which is 36.

What you need to implement

In the first part,we begin with a simple interface called Expression:

(this interface uses generics and map)

public interface Expression {
   // Evaluate the expression using the variable values provided
   // in the assignment, and return the result.  If the expression
   // contains a variable which is not in the assignment, an exception
   // is thrown. 
   double evaluate(Map<String, Double> assignment) throws Exception;

   // A convenience method. Like the `evaluate(assignment)` method above,
   // but uses an empty assignment.
   double evaluate() throws Exception;

   // Returns a list of the variables in the expression.
   List<String> getVariables();

   // Returns a nice string representation of the expression.
   String toString();

   // Returns a new expression in which all occurrences of the variable
   // var are replaced with the provided expression (Does not modify the
   // current expression).
   Expression assign(String var, Expression expression)
}

You should write following classes, each of them corresponding to an atomic expression, and each of them should implement the Expression interface.

• Num, Var -- representing numbers and variables.
• Unary expressions: Sin, Cos, Neg.
• Binary expressions: Plus, Minus, Mult, Div, Pow, Log.

The Log(b, x) function is the log of x in base b, for example Log(2,8) = 3. The Neg(x) function is the negation, for example Neg(1) = -1 and Neg(-1) = 1.

Num should have a constructor accepting a double. Var should have a constructor accepting a String. The unary expressions should have a constructor accepting an Expression. The binary expressions should have a constructor accepting two Expressions.

The implementation will make heavy use of recursion. For example, in order to evaluate an expression, you need to first evaluate its sub-expressions and then apply some function to the results, with the base cases being the evaluation of the Var and Num expressions.

Constructor Shortcuts

In order to make it easier to create expressions, add also constructors that provide "shortcuts" for creating the Num and Var classes. For example, instead of writing new Plus(new Var("x"), new Num(5)) we would like to be able to write new Plus("x", 5) and get the same resulting expression.

Class Hierarchy

You should also implement the abstract base classes BaseExpression, UnaryExpression and BinaryExpression, and have the different expression classes inherit from them, according to the following hierarchy:

Try to put shared code in the base classes instead of the leaf classes. Example for candidate methods that can be in the base classes are double evaluate() and List<String> getVariables(). You can add whatever non-public methods you want to the class hierarchy in order to help with code sharing.

How to approach this

You need to implement many classes. One way to approach this would be to start with only a subset of the classes, for example only Var, Num, Plus and Minus. Once these are working, see if you can move some of the shared code to the base classes UnaryExpression, BinaryExpression and BaseExpression. Then, go ahead and implement the rest of the expression classes.

Test your code

Create a class with a main method that creates some nested expressions (for example Expression e as defined above) and then prints them, evaluates them, and asks for the variables in them).

Part 2 -- Automatic Differentitation

We can now create expressions, get their variables, and evaluate them with given variable assignments.

In this part we will also differentiate them according to a given variable.

Add the following method to the Expression interface:

public interface Expression {
   // ... as before
   
   // Returns the expression tree resulting from differentiating
   // the current expression relative to variable `var`.
   Expression differentiate(String var);
}

For example:

Expression e = new Pow(new Var("x"), new Num(4));
Expression de = e.differentiate("x");
System.out.println(de); // we expect to see 4*(x^3)
// but seeing: ((x ^ 4.0) * ((1.0 * (4.0 / x)) + (0.0 * log(e, x))))
// is also fine, as it is equivalent (we will improve it in the next part).

If your calclus is a bit rusty, the Wikipedia page for differentiation rules has a useful summary.

Dealing with mathematical constants

What do we do with constants like e or Pi that can take part in definition of expressions, and that can also arise when computing derivatives? One option is to just treat them as variables, so e will be new Var("e"). This is consistent with the mathematics, and is a good modeling of the problem. And when someone wants to compute the value of the expression, they can either assign a value to the variable (setting e to 2.71828 or a similar value) or leave it as a variable. It is up to the user to assign the correct value when evaluating the expression. Taking this approach in this assignment is perfectly fine.

An alternative approach is to introduce a new type, called Const that will be initialized upon construction with both its name and its value (new Const("e", 2.71828)). You can also use this approach if it is more convenient or feels more natural to you.

Part 3 -- Simplification

If you tried to differentiate some non-trivial expressions using your code from part 2, you probably noticed that while the resulting expressions are (hopefully) technically correct, they are also quite messy and contain many "redundant" parts. For example:

Expression e = new Pow(new Plus(new Var("x"), new Var("y")), new Num(2));
System.out.println(e.differentiate("x"));
// the result is:
// (((x + y) ^ 2.0) * (((1.0 + 0.0) * (2.0 / (x + y))) + (0.0 * log(e, (x + y)))))

This is correct, but really hard to read. We need to "simplify" the expression to make it more friendly to humans.

We will add another method to the Expression interface. This method will return a new expression which is a simplified version of the current one.

public interface Expression {
   // ... as before

   // Returned a simplified version of the current expression.
   Expression simplify();
}

Example usage:

Expression e = new Pow(new Plus(new Var("x"), new Var("y")), new Num(2));
System.out.println(e.differentiate("x"));
// the result is:
// (((x + y) ^ 2.0) * (((1.0 + 0.0) * (2.0 / (x + y))) + (0.0 * log(e, (x + y)))))
System.out.println(e.differentiate("x").simplify());
// the result is:
// (((x + y) ^ 2.0) * (2.0 / (x + y)))

e = new Pow(new Var("e"), new Var("x"));
System.out.println(e.differentiate("x"));
// ((e ^ x) * ((0.0 * (x / e)) + (1.0 * log(e, e))))
System.out.println(e.differentiate("x").simplify());
// (e ^ x)

While the result is not as simple as 2*((x + y)^2), it is much simpler than before.

You need to support the following simplifications:

• x * 1 = x
• x * 0 = 0
• x + 0 = x
• x / x = 1
• X / 1 = x
• X - 0 = X
• 0 - X = -X
• X - X = 0
• log(x, x) = 1
• an expression without variables evaluates to its result. ((2*8)-6)^2 => 100.

Note that X here stands for any expression, not just a variable. In particular log(x,x) = 1 and x - x = 0 should work for any case where the two arguments are equal to each other.

These should be recursive, so that, for example: (log(9x, 9x)*2y) => 2y and ((3+6)*x + (4x * sin(0))) => 9x.

Part 4 -- advanced simplification

This part is a bonus. You can get full grade on this assignment also without the bonus, but implementing it will give you up to an extra 25 points (so the final grade for this assignment can be 125).

The simplification you implemented in Part 3 was useful, but still leaves a lot to be desired. In this part, you will improve the simplification mechanism to make it more powerful.

Your job is to make the best simplification possible, so that you get the most compact expressions.

Some candidate for simplifications are:

• (x^y)^z => x^(y*z)
• ((2x) + (4x)) => 6*x
• nested expressions ((2x) + (2 + ((4x) + 1))) => 6x + 3

But the sky is the limit.

Note that unlike in the previous section, in the more advanced simplifications we cannot work only at the Expression level: for example when simplifying (x^y)^z, is it not sufficient for the outer Expression Pow(Pow(x,y), z) to know that the inner Pow(x,y) is an Expression -- we want to give special treatment to inner expressions of type Pow. For this, we can use the instanceof keyword:

Expression e = new Var("x");
if (e instanceof Var) {
   // something
} else {
  // ...
}

It is usually not ok to use instanceof in object-oriented code, but in this particular problem, it is really very hard to avoid it. So we allow its use in this case. (An alternative would be to add methods such as "isPower()", "isPlus()" and so on to the interface and checking on them instead of using instanceof, but this is not really "solving" the problem).

Hint: the third simplification we suggest relies on the distributive and associative rules. You may want to create other types of expressions (not necessarily binary) in order to help with the simplification process. In general, you can create any number of extra classes or interfaces that may help you achieve your goal.

What to submit:

Your code should include at least the following classes, interfaces and abstract classes: Num, Var, Sin, Cos, Neg, Plus, Minus, Mult, Div, Pow, Log. Expression, BaseExpression, BinaryExpression, UnaryExpression.

You should also include a class called ExpressionsTest including a main method that will:

1. Create the expression (2x) + (sin(4y)) + (e^x).
2. Print the expression.
3. Print the value of the expression with (x=2,y=0.25,e=2.71).
4. Print the differentiated expression according to x.
5. Print the value of the differentiated expression according to x with the assignment above.
6. Print the simplified differentiated expression.

Each printing should be performed on its own line, do not add extra text, and do not add spaces between the lines.

Your makefile should have a run target to run the ExpressiosTest main class.

String representation rules

• Num can have floating point: 2.0
• Spaces and parenthesis in Binary +,-,*,/: (x + y), (x * y), (x - y), (x / y)
• Parenthesis (but no spaces) in ^: (x^y)
• Space after comma in Log: log(x, y)
• Neg: (-x)
• Sin, Cos: sin(x) (can have double parenthesis if they come from the inner expression)

If you did the bonus:

Same as above, but also submit:

• A text file (NOT .doc, plain ascii English text) called README.txt describing the kinds of simplifications you did and the approach you took to do them.
• A file called SimplificationDemo.java with a main that demonstrates your simplification (and prints out pairs of non-simplified and simplified expressions).
• Your makefile should include a target called "bonus" that will run your SimplificationDemo class.
• Note that a large part of your nouns grade will be determined based on the quality of the explanations in the README.txt file, and on the examples in the SimplificationDemo.java program and its output. You need to convince that you did something cool. (Of course, you also have to actually DO something cool. But if you implement the best simplification ever but don't describe and demonstrate it properly, it will not be sufficient).